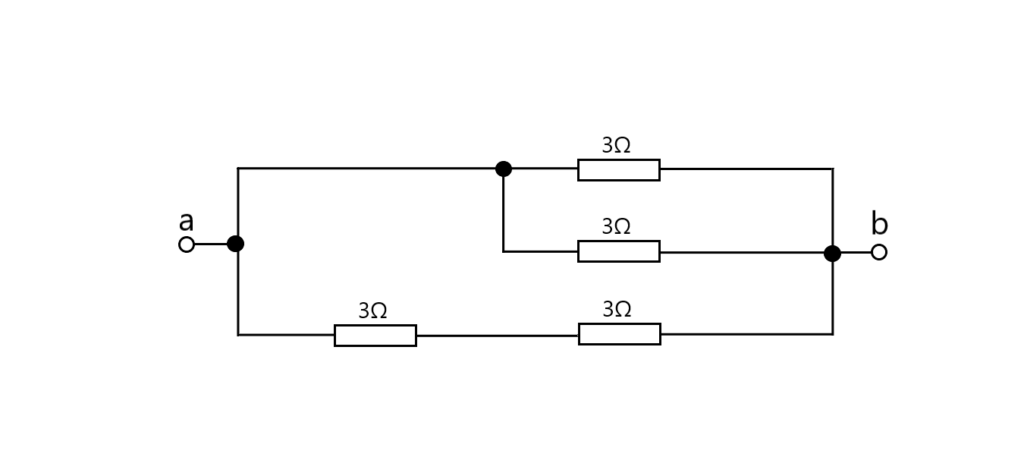
問3.図のような回路で、端子aーb間の合成抵抗[Ω]は。
イ.1.0 ロ.1.2 ハ.1.8 ニ.2.0
直列接続の合成抵抗値は、\(R=R1+R2+R3+・・・+Rn \)[Ω]。足し算です。
並列接続の合成抵抗値は、\( R=\dfrac{1}{\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}・・・\dfrac{1}{Rn}} \)[Ω]。分数の中に分数が入ってます。なぜかはわからないけど、公式覚えて計算すればいいので、まあ良しとしましょう。
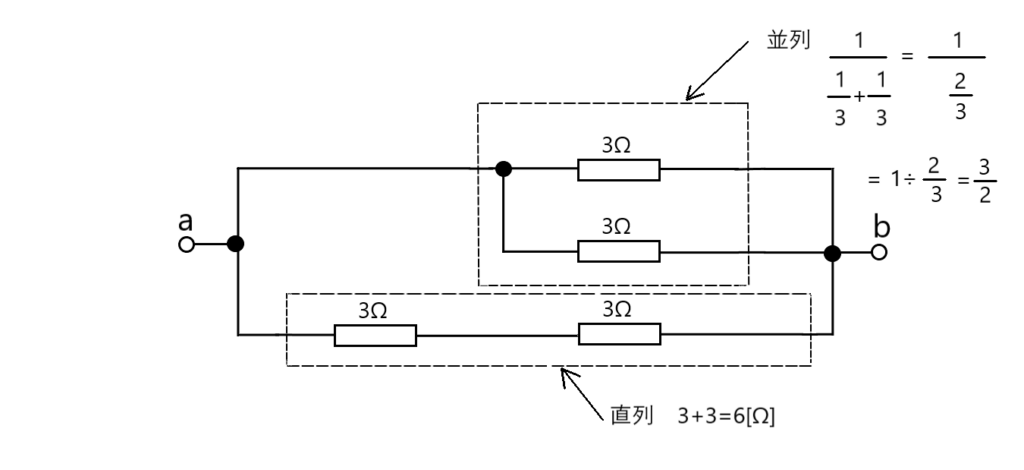
まずは簡単なところからやっていきましょう。下は直列なので簡単!3たす3で6おーむ、と。
上は並列。ちょっと嫌な感じだけど、\( \dfrac{1}{3} \)、分母が同じなので、なんとかなりました。
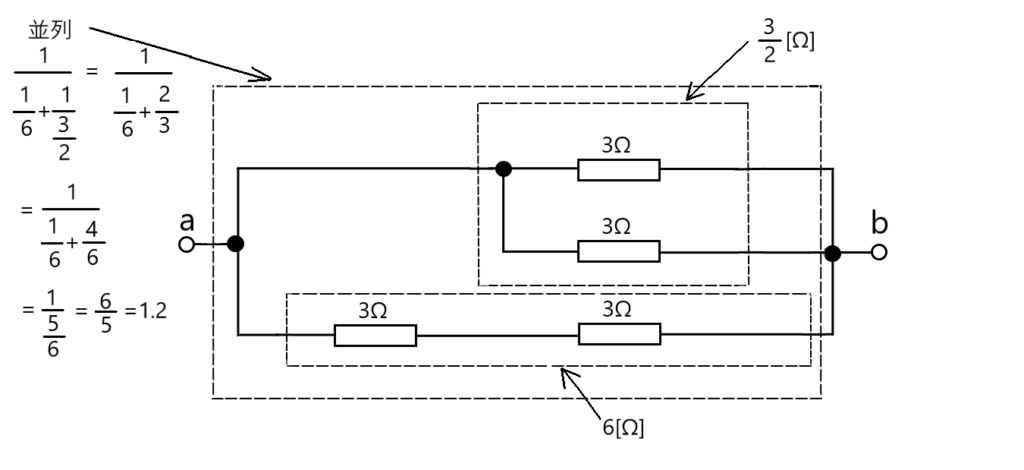
さあ仕上げ、最後は並列。なんか、分数の中に分数が入って、さらに分数がはいるというわけわかんないことになるんですけど、こんな式ははたして正式に存在するのでしょうか。でもめげずに落ち着いてやってみたら、結構いけますね。
答え、ロ.1.2で合いました!
ちなみに、「和分の積」というのがあります。
\( R=\dfrac{1}{\dfrac{1}{R1}+\dfrac{1}{R2}} \)は、\( R=\dfrac{R1×R2}{R1+R2} \)
というのです。\( R1 \)=\( R2 \)で、2個の時しか使えないんですけどね。
これでやると、\( \dfrac{1}{\dfrac{1}{3}+\dfrac{1}{3}} \)=\( \dfrac{1}{\dfrac{2}{3}} \)=\( \dfrac{3}{2} \)のときに、\(\dfrac{3}{2} \)を小数点にして\( 1.5 \)とし、\( \dfrac{6×1.5}{6+1.5} \)=\( \dfrac{9}{7.5} \)にして、\( 9÷7.5=1.2 \)として出します。式としては幾分すっきりしています。でも和文の積、覚えなきゃいけない、でも、こっちの方が速そう。