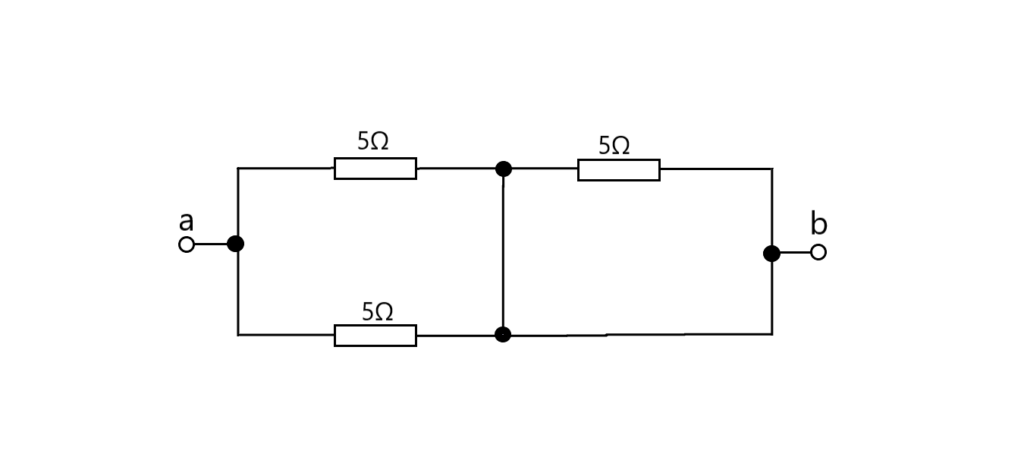
問4.図のような回路で、端子aーb間の合成抵抗[Ω]は。
イ.2.5 ロ.5 ハ.7.5 ニ.15
私はアホの子。あっさりだまされる女。
並列接続の合成抵抗値は、\( R=\dfrac{1}{\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}・・・\dfrac{1}{Rn}} \)[Ω]、でしょー、どっちも\( 5Ω \)だから「和文の積」\( R=\dfrac{1}{\dfrac{1}{R1}+\dfrac{1}{R2}} \)は、\( R=\dfrac{R1×R2}{R1+R2} \)、使っちゃてー、\( \dfrac{5×5}{5+5} \)=\( \dfrac{25}{10} \)で、\( 2.5 \)よね。
直列接続の合成抵抗値は、\(R=R1+R2+R3+・・・+Rn \)[Ω]。だから、\( 2.5+5=7.5 \)。ほっほー楽勝ーーー、ハ.7.5ね、って、違うんかーーーい!正解はイ.2.5です。
どうもね「短絡」というのがあって、b側の抵抗には電流が流れないらしいんですわ。
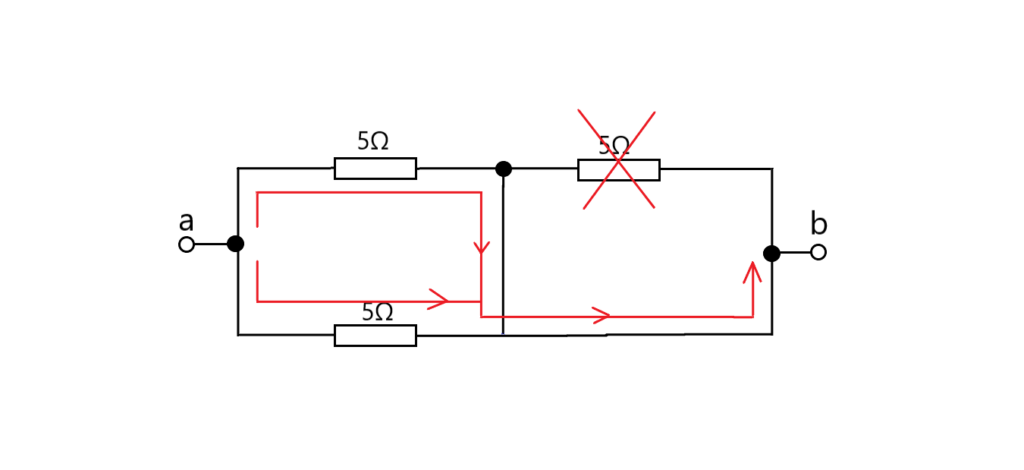
なんじゃそりゃ。”抵抗”というだけあって、電流も流れを妨げるような物があるところは避けて、障害物が無い選択肢がある場合は、そっちにだけ流れるということですかね。嫌なものは避け、安きに流れるのは私と同じか。なので、結局↓こういう事になり、
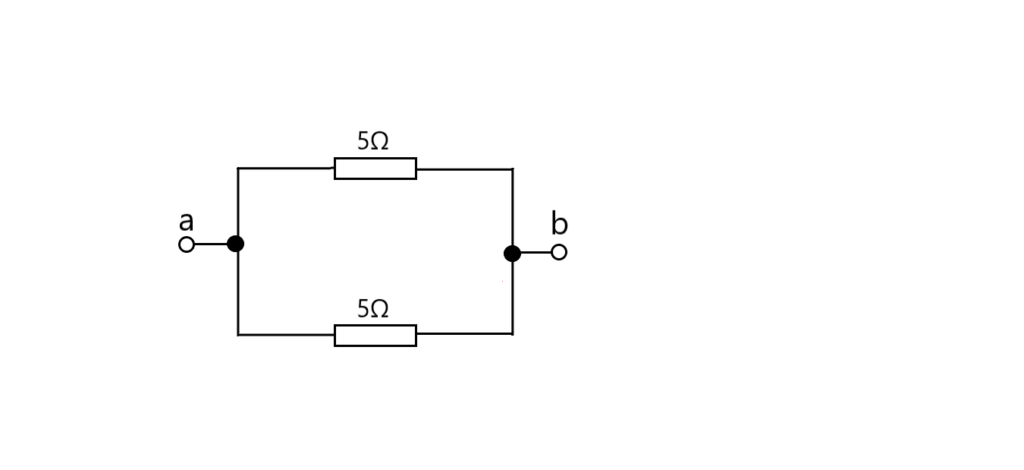
並列接続の合成抵抗値は、\( R=\dfrac{1}{\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}・・・\dfrac{1}{Rn}} \)[Ω]、でしょー、どっちも\( 5Ω \)だから「和文の積」\( R=\dfrac{1}{\dfrac{1}{R1}+\dfrac{1}{R2}} \)は、\( R=\dfrac{R1×R2}{R1+R2} \)
使っちゃてー、\( \dfrac{5×5}{5+5} \)=\( \dfrac{25}{10} \)で、\( 2.5 \)よね。
で、終ー了ー、でよいのでした。